druban wrote:...A very wild guess is that you have mistaken my idea to mean that the radius value I proposed should also double as the radius of the arc constructed on the corner. This would almost never be the case for non-right angles although I would not want to go out on a limb and actually say impossible. ...
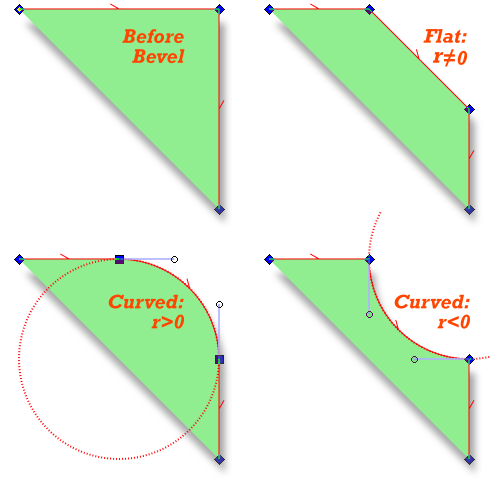
The image shown in the second post of yours in the topic has the writing r=/=0 at the flat bevel, and two curved ones with r>0 and r<0.
I thought of it as you give r as a basic input to your bevel tool.
I assumed that every bevel method as you mentioned -positive or inverse, and the flat one- was managed by the r, they should work with the same method.
Thus I was thinking of it as r<o is an incorrect form. No lenght, no curvature can be less then zero, so I came up with the solutions on my first image of that post.
druban wrote:...Another guess is that you think the same arc radius should work for every node in a path, which would also be very unlikely. The radius of the arc rounding the corner would have to be derived from a construction (using two tangents) far less hair-raising than the ones implied by your illustrations...
Thinking of the actual use, how would you make any user to use only paths with straight lines, and avoid selecting more nodes than one at the same time?
I think it would be a fair to expect that from a tool like that.
druban wrote:...Are you saying that concave corners would not be continuous with the curve before and after? This I completely agree with. The only way to construct concavity would be to make the rounded corvexity and then reflect the circle across the endnodes. No other interpretation, to me, could be anything but random. My verbal description of the process is sorely lacking, I fear....
I wasn't thinking of concave corners yet.
druban wrote:...The final illustration seems to imply that a curve can have several tangent circles at the same point, a phenomenon possible in mathematics of a much higher order than I can claim familiarity with. Did you look at the various methods proposed elsewhere in this forum for manual solutions to the rounding problem using geometric construction, only two of which I provided links for in my incurable laziness? I shall take another look at them to see if I can find any obvious error in them.... I felt it sufficient to provide a link to the thread that shows a way - (mine, therefore perhaps inaccurate) of how to construct an arc that rounds a corner to a particular size, rather than repeat the whole tedious explanation.
There can be only one exact tangent in this case.
I didn't look for constructing tangent circles for curved paths. That would be impossible to do in an accurate way of its nature.
Bezier splines are approximations of points rendered to the actual display, and, drawing tangents to it would need the knowledge of every point with curvatures.
Anyway, constructing tangent circles to circles can be complicated geometrically alone.
That many circles on the image that might made you think that was about to show more bevel options.
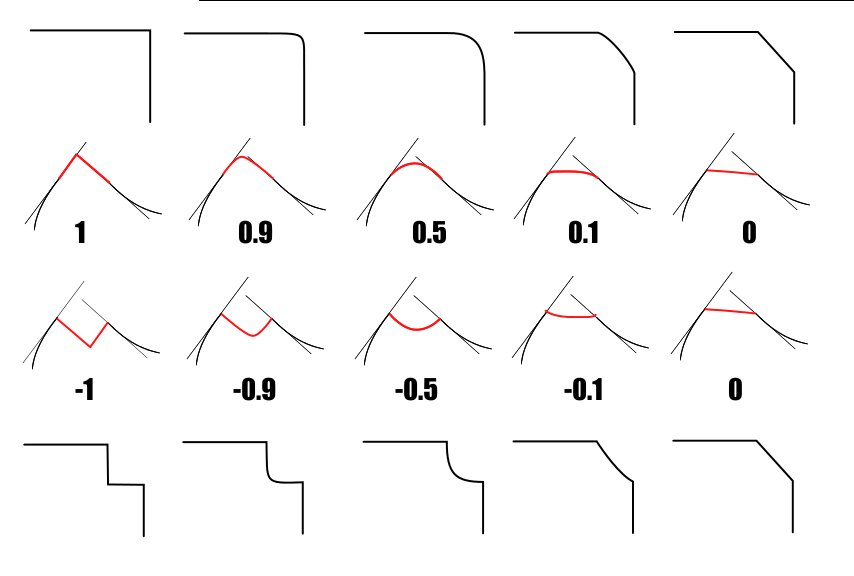
By the positive, flat and inverse rounded corners, comes a question of how the inverse corners would be presented.
As, they have little visual connection with the positive rounded bevels, I was thinking, why not to have an option of different outsetting of the arch's origo?
Then again as I tried to describe above thinking of origos and radiuses is not an efficient way of making such a bevel, as there would be problems with the minimal and with the maximal radius lengths.
 control bar that automatically does all these steps I do manually! So here are my suggestions.
control bar that automatically does all these steps I do manually! So here are my suggestions. This is a read-only archive of the inkscapeforum.com site. You can search for info here or post new questions and comments at
This is a read-only archive of the inkscapeforum.com site. You can search for info here or post new questions and comments at